Affine Combinations

If you have at least two vectors, you can usually express a third one as a linear combination of the first two.

$\vec{v_3} = c_1\vec{v_1} + \cdots + c_2\vec{v_2}$

Affine combinations are an extension of linear combinations where the coefficients must sum to one.

$c_1 + \cdots + c_n = 1$

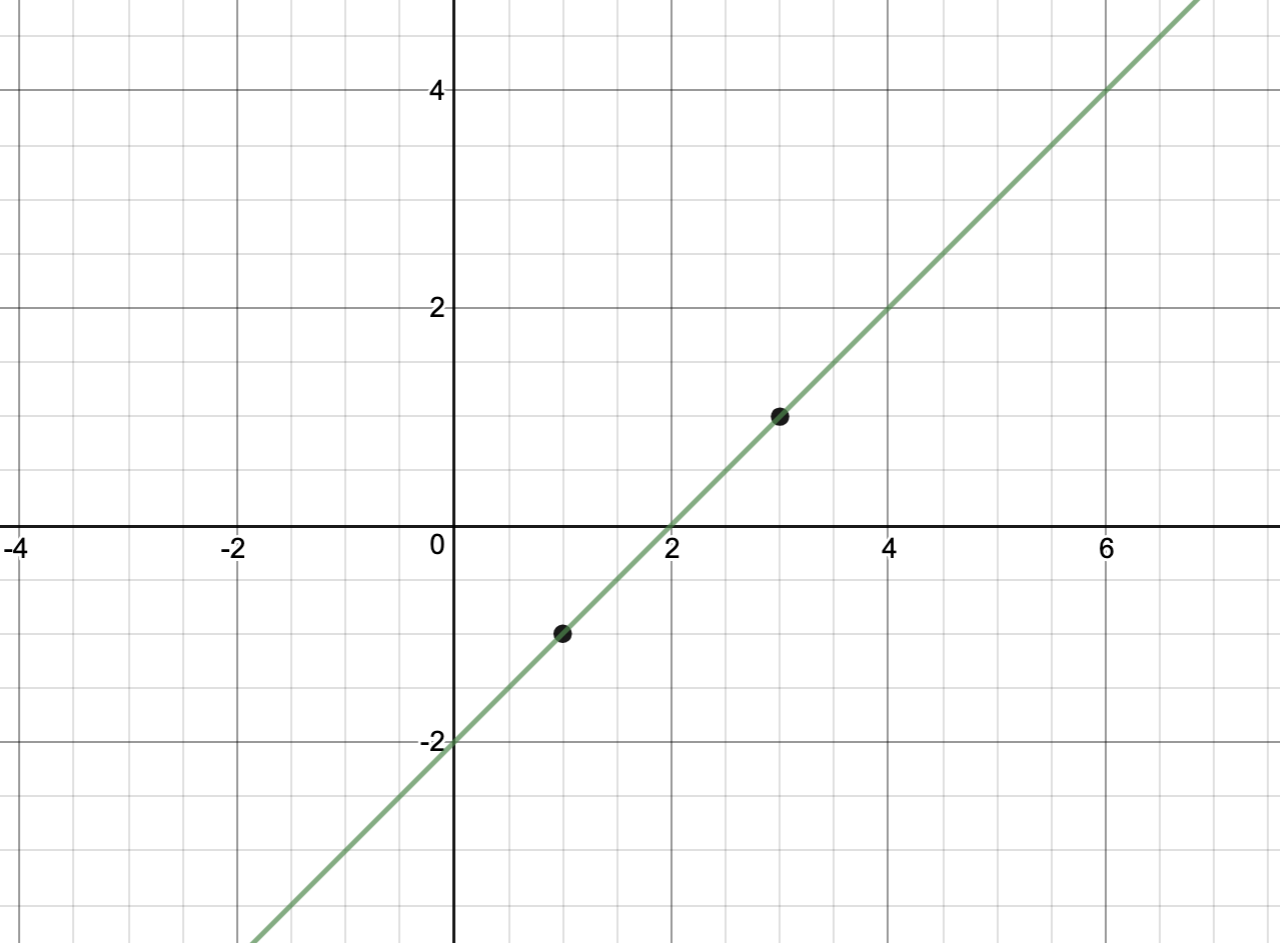
This limitation makes way to some interesting ideas. We can deffine an affine hull of some given vectors as $\operatorname{aff}(\vec{v_1}, \cdots, \vec{v_n})$ The affine hull of a set of vectors is the set of all possible affine combination. This is almost like a subspace, but it does not have to include the origin. The affine hull intersects the vectors. It is more intuitive to think about the vectors as points instead of directions.

The affine hull of two vectors (points) in $\R^2$ looks like this.